初识神经网络

为什么 AI 能够自主学习纠正自己的行为？本质上 AI 学习的过程同人类相似，都是基于基础的神经元结构。人脑通过将大量的神经元细胞连接在一起组成神经系统，AI 同理，通过将大量人工神经元节点组合形成神经网络。神经网络内部使用了某种协作机制实现了神经网络的参数自我调节——即自主学习。

神经元模型

神经元是构成神经网络的基本组成部分。神经元本质上描述了一组输入和输出的关系。

感知机

以最简洁的神经元模型——感知机为例，感知机模型类似于计算机中的逻辑门模型（与，或，非，异或），对于感知机来说，可接受多个任意值作为输入，但仅输出 0 和 1。

$$output=\{\begin{array}{llc}0& & \text{if }{\sum }_j{w}_j{x}_j\le threshold\\ 1& & \text{if }{\sum }_j{w}_j{x}_j>threshold\end{array}\text{\hspace{1em}(1)}$$

对于任意输入$x_j$，当且仅当 ${\sum }_j{w}_j{x}_j$ 大于阈值 $threshold$ 时才输出 1，反之输出0。其中 $w_j$ 表示对于 $x_j$ 来说，对应的输入权重，通俗解释为对于输入 $x_j$ 来说，其作为输入值对于整个感知机输出来说有多重要。越重要的 $x_j$ 对应的 $w_j$ 越大，反之，越小。 为了简化多个感知机的计算过程，将公式1化整为公式2：

$$output=\{\begin{array}{llc}0& & \text{if }w\cdot x+b\le 0\\ 1& & \text{if }w\cdot x+b>0\end{array}\text{\hspace{1em}(2)}$$

其中，定义 $w\cdot x\equiv {\sum }_j{w}_j{x}_j$，$b$ 表示偏置 ，且 $b\equiv -threshold$。在感知机中引入偏置是为了衡量神经元在没有接受到任意输入时，有多容易靠近激活的输出值。 为了便于在叠加多个感知机时的计算操作，使用 $h$ 函数抽象感知机的内部激活过程，那么最终感知机的输入与输出关系可被归纳为

$$Perceptro{n}_{output}=h(w\cdot x+b)\text{\hspace{1em}(3)}$$

其中 $h$ 函数这一类抽象了神经元激活过程的而函数被称为神经元的激活函数。

激活函数

从数学上来说，我们可以使用任意激活函数来表示单个神经元模型。如图示，同感知机模型一样，$h$ 函数接受任意个输入作为函数参数，在其函数内部经过一系列计算输出 $y$， $y$ 不仅是函数 $h$ 的输出值也是对应神经元的输出值。

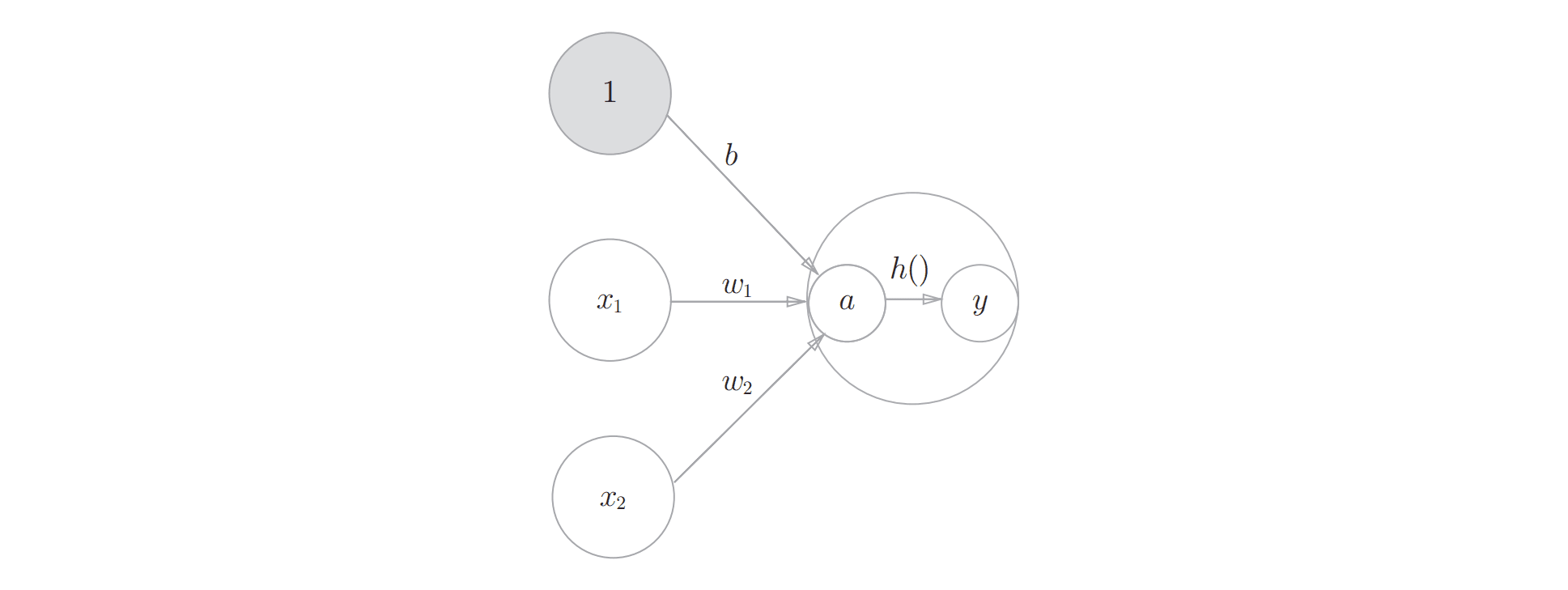
不同类型的神经元之间的差异主要体现在激活函数不同。在神经网络中，对于不同层的神经元，激活函数可相同，可不同。常见的激活函数有阶跃函数，sigmoid 函数，ReLU 函数等非线性函数。特别地，存在一类特殊神经元——输出层神经元。它们一般使用 softmax 函数或恒等函数作为激活函数。

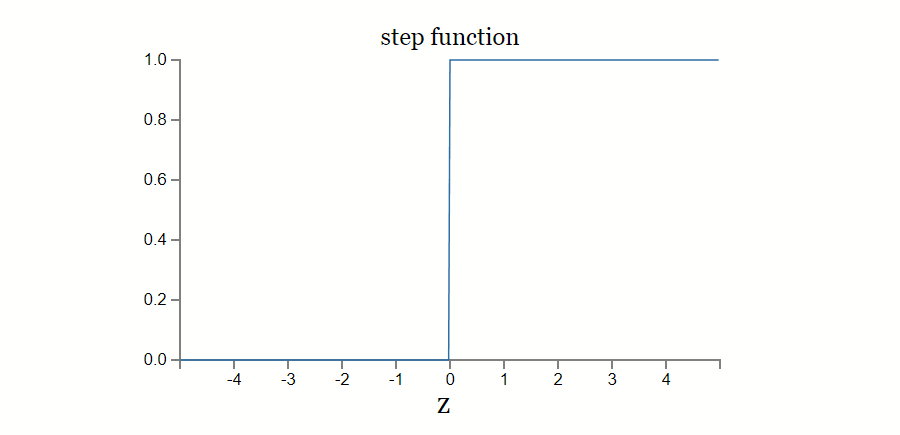
阶跃函数

阶跃函数是最简单的激活函数。它表示了一种仅当输入达到一定阈值时才切换输出的一种神经元激活过程——朴素感知机。其主要缺陷同朴素感知机一样只能表达二元值问题，无法表达多元值问题。而在实际应用场景中大多数问题都是多元值问题。

sigmoid 函数

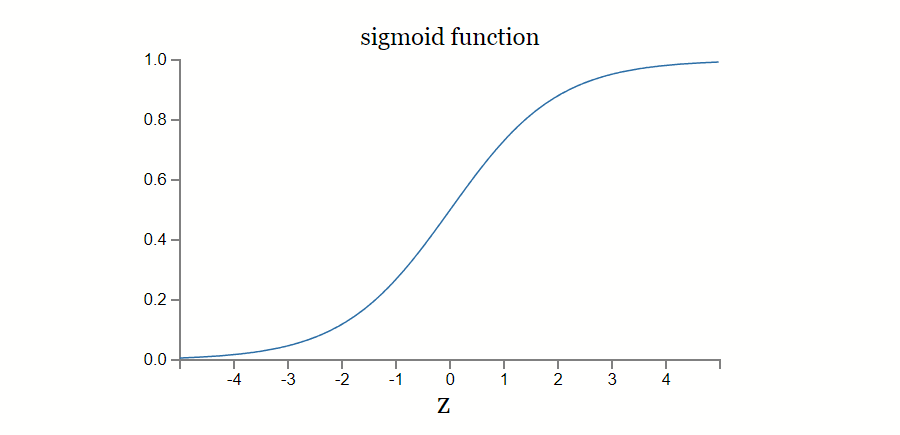
一种经典的实践是基于 sigmoid 函数所代表的神经元。其数学形式：

$$\sigma (z)\equiv \frac{1}{1+e^{-z}}\text{\hspace{1em}(4)}$$

sigmoid function 相对于阶跃函数的主要优势是，输出值的取值范围不再是离散的，而是连续的 [0, 1] 区间。

激活函数的非线性空间

一般我们使用非线性函数作为神经元的激活函数。为什么非线性空间是必须的？通过反证法证明，线性空间只是输入与常量的乘积叠加，无法表达输入与输出的非线性关系。

线性激活函数神经元的问题在于神经元的叠加始终可被单层线性神经元等价。以线性函数 $h(x)=cx$和$a(c)=c^3$ 为例，其中 $c$ 为常数，那么叠加3层 $h$ 的神经网络效果与单层 $a$ 神经元效果相同，那么之前叠加神经元没有起到任何叠加效果：

$$y=h(h(h(x)))\to c\times c\times c\times x\to ax\text{\hspace{1em}(5)}$$

而如果激活函数是非线性函数时，上述推论不成立，那么通过叠加多层神经元可表示复杂的非线性关系。

我们需要解决的实际分类或归纳问题大多也都是非线性问题。换句话说，为了追求输出空间的灵活性，且能够应对复杂的输入和输出关系，我们一般使用非线性函数作为神经元的激活函数。

神经网络

在我们对神经元模型有了基本了解后，叠加多个神经元即可组成一个简单的神经网络。在神经网络中，一个神经元的输出也是另外一个神经元的某个输入。通过调节某个神经元的某个输入权重或偏置时，将引起一系列连锁反应，最终反映在神经网络的输出变化中。

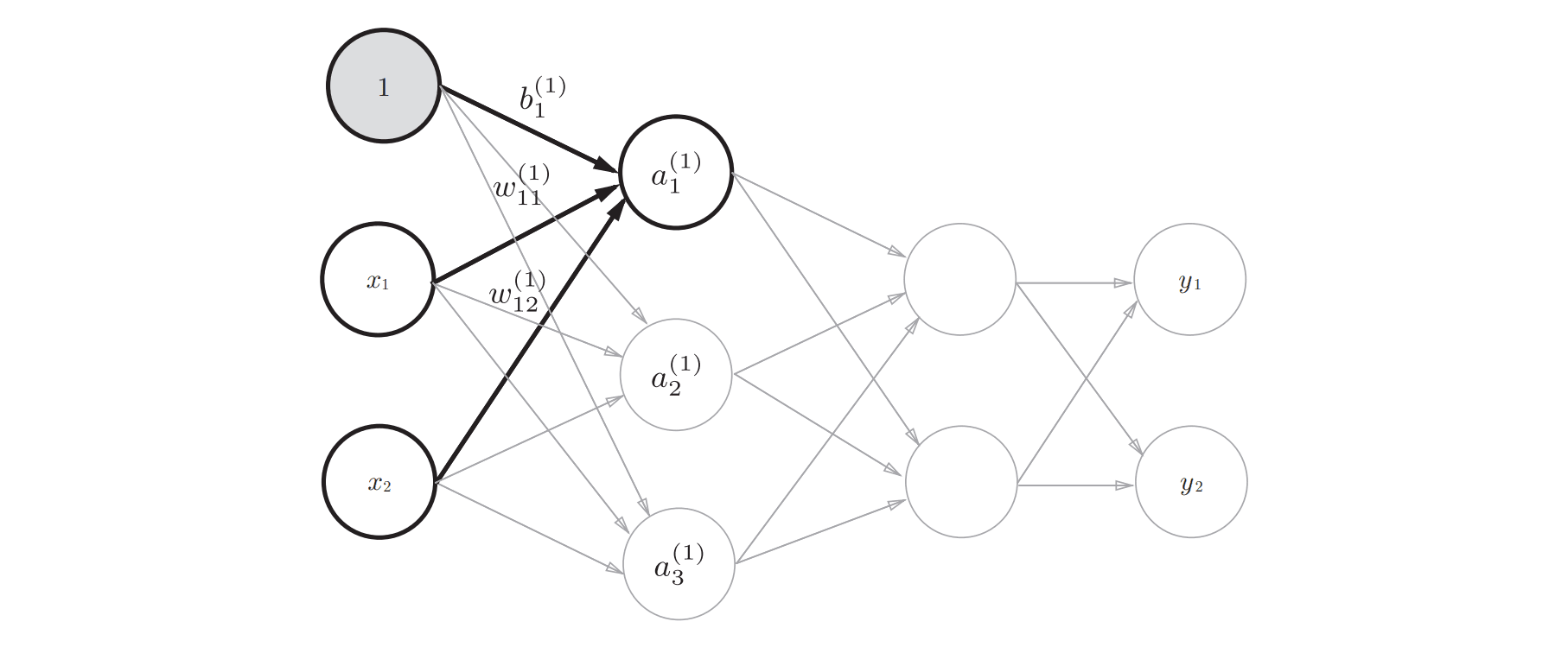
在神经网络的组成上，一般存在多层神经元，单层神经元由多个神经元构成。从左至右，最左一般为输入层神经元，最右称为输出层神经元，中间的其他层神经元称为隐藏层神经元。

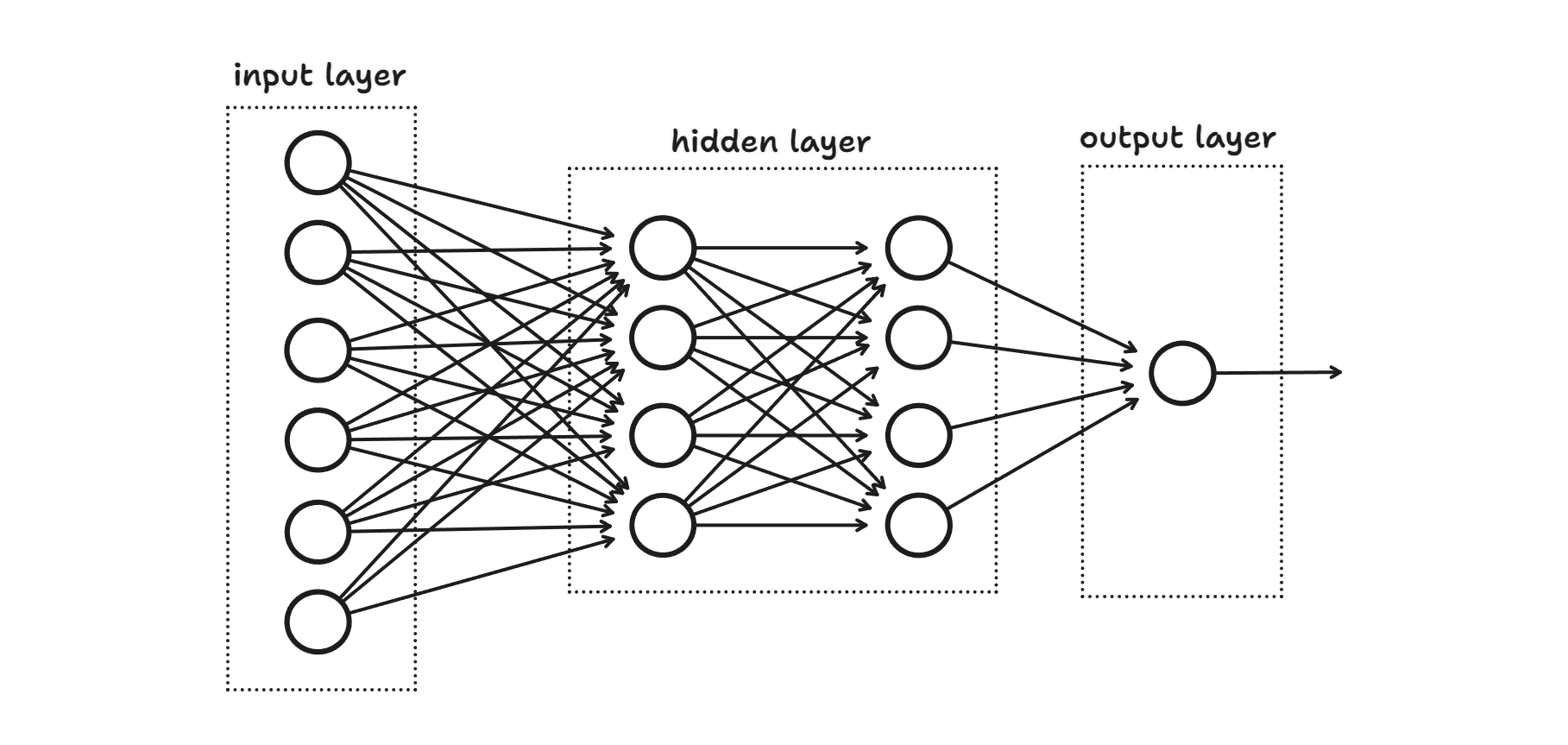
在简单的神经网络中，当我们通过调整输入层神经元的权重或偏置，将引起神经网络中各层神经元的输入输出的连锁反应。理想情况下，通过不断的调整权重或偏置参数，能够帮助神经网络的输出值不断靠近正确解。难点在于如何找到一种合理的机制帮助判断如何调整神经网络的权重和偏置参数？对于微型神经网络，最简单直接的方式就是人工进行调整参数。但一般我们所面对的神经网络都异常庞大，对于具有成千上万个权重和偏置的神经网络，人工调节单个神经元权重和偏置参数显然不现实。我们期望神经网络能够自主根据某项规则自动调节神经元的权重和偏置参数——从数据中进行自我学习。

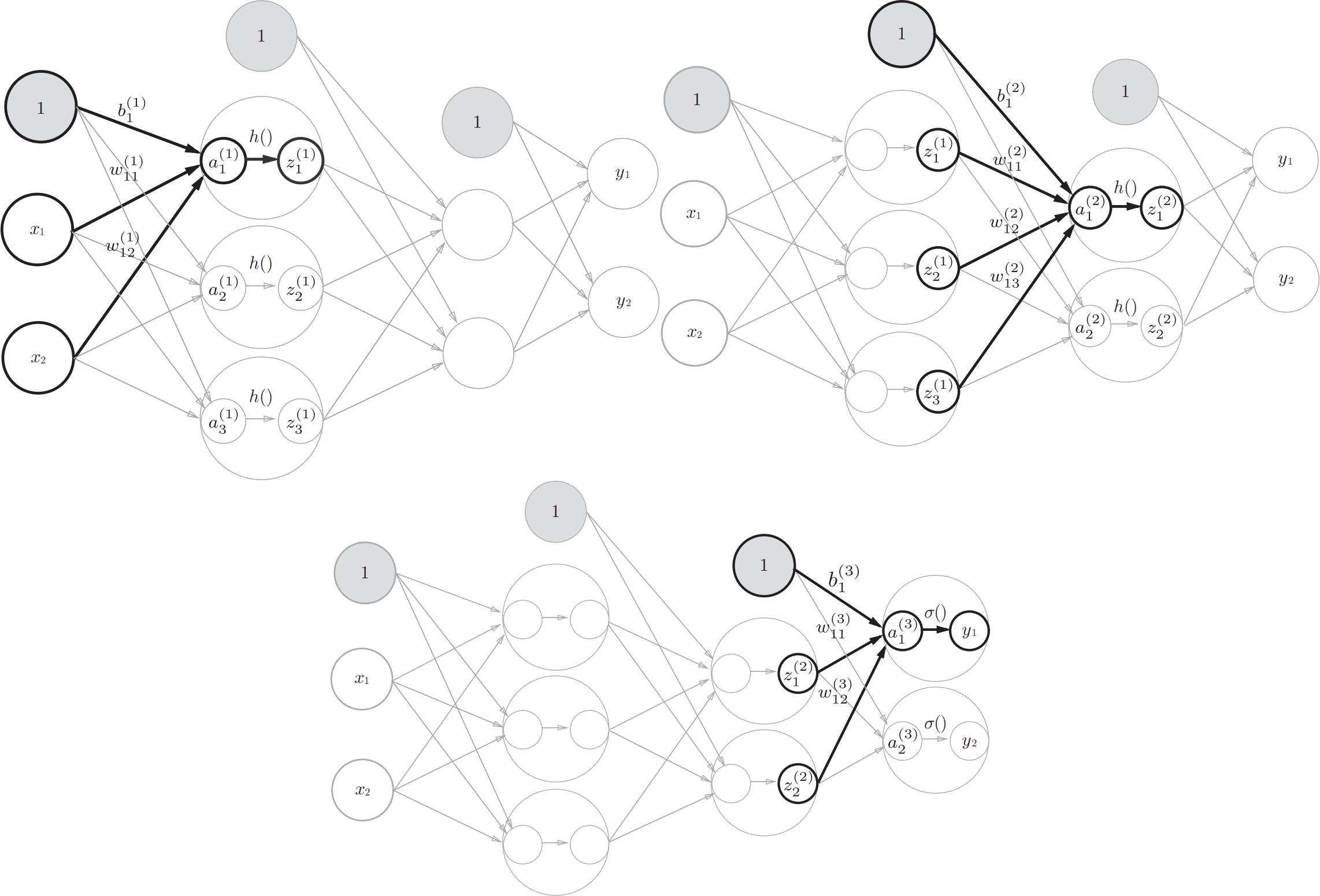
损失函数

神经网络以模型的泛化能力作为学习目标。神经网络自我学习的过程本质上就是不断更新各个神经元输入参数的权重和偏置参数。为了能够实现自我更新参数，那么神经网络必须具备量化当前神经网络输出与正确解的差异。以差异值作为指引，不断尝试更新权重和偏置参数值以最小化与最优解之间的差异，最终使得神经网络输出不断逼近最优解。

为了量化神经网络输出值与实际真实值的偏差，我们引入损失函数作为评估输出结果的量化工具。当损失函数输出值越小时，表明神经网络的输出值越靠近真实值，反之越偏离真实值 。

为什么不直接使用识别精度作为偏差的量化指标？例如，100 个数据中正确识别了 50 个数据，通过调整权重或偏置，期望提升识别率，识别比 50 个更多的数据？因为在复杂神经网络中，微小的权重和偏置变化，要么不足以对识别精度产生影响，要么会产生不连续的剧烈变化，导致无法有效的缩小神经网络参数的取值范围。

理想情况下，我们期望的是存在一种能够体现连续的正确解差异的量化方式，以帮助更新权重和参数值。而这种方式正是前文提到的损失函数。常见的损失函数有交叉熵误差和均方误差，一般交叉熵误差损失函数使用较多。

• 均方误差 $E=\frac{1}{2}{\sum }_k(y_k-t_k{)}^2$，其中 $y_k$ 表示神经网络的输出，$t_k$ 表示监督数据，$k$ 表示数据维度。
• 交叉熵误差 $E=-{\sum }_k{t}_k\ln y_k$，其中 $y_k$ 表示神经网络的输出，$t_k$ 表示监督数据，$k$ 表示数据维度。

加速损失函数计算

由上我们了解了评估神经网络学习效果的方法，其中有一个显著特点是每次调参所有神经网络节点都需要参与。这种方式虽然精确，但效率底下。当神经网络的数据集非常大时，每个数据输入到神经网络中的话会耗费大量计算时间，为了提效神经网络的学习过程，我们可以对数据集进行随机抽样，这种以抽样代表性数据集训练的方法称为 mini-batch 学习，此举可极大降低神经网络学习的计算量。

最小化损失函数

结合前文的学习目标，为了使得神经网络的泛化能力不断提升，我们需要使得损失函数的输出值尽可能小。那么如何基于损失函数调整权重和偏置？求函数最小值？对于具有成千上万个输入参数的损失函数，基本无法直接求得最小值。

对于损失函数极小值问题，我们使用导数来解决。为了使得神经网络的输出尽可能逼近正确解，那么我们需要损失函数的输出值尽可能小，而为了使得输出值尽可能小，对应其函数图像一定处于导数趋近于 0 的点。不断循环往复以导数作为指引，逐步更新神经网络权重和偏置参数值。

梯度下降法

对于存在多参数的函数偏导，我们定义，所有参数的偏导构成的元组称为梯度，本质上梯度对应了坐标系中的一组向量，该向量的方向始终是函数值减小最多的方向。那么我们根据向量的方向可不断逼近函数图像的鞍点（一定是极小值或最小值点）。

对应到神经网络的参数更新过程，根据梯度的方向，不断调整神经网络的权重和偏置参数值，进而得到新的神经网络新的输出，并使用损失函数计算新的梯度，根据新的梯度再次更新神经网络参数，如此往复，在经历一定的学习迭代次数后，神经网络的参数此时已经能够将损失函数的值降到最小，换句化说，神经网络新的输出值和正确解的差异达到最小了。梯度下降权重参数更新的数学表示如下：

$$x_i=x_i-\eta \frac{\partial f}{\partial x_i}\text{\hspace{1em}(5)}$$

在上述学习过程中，每次的梯度更新量 $\eta$ 被称为神经网络的学习率，过大和过小的学习率均无法达成良好的学习效果。过大的学习率会导致输出值发散，反之在到达指定学习轮数后，可能参数的更新范围还很小，对于神经网络的学习基本没有产生什么影响。